Gelosia Method
This was brought over as a method from India to Europe in the 14th century, with Gelosia meaning ‘lattice’ from the trellis work on windows in Italy. John Napier based his set of bones on this Gelosia arrangement on a grid.
What are the advantages?
- You are only dealing with multiplication facts up to 9x9 and addition
- It looks quite tidy and efficient - it is surprisingly quick.
Any disadvantages?
- It looks like a trick – difficult to see the reason why it works
- Easy to forget the ‘carried’ number
- You need lattice paper for the layout
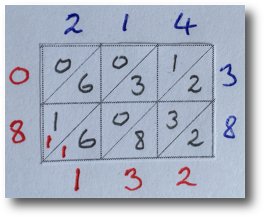
Here is how to calculate 214 x 38.
1. Using the lattice squares with diagonals drawn on them, write 214 along the top and 38 down the right of the grid, with one digit for each square.
2. Start with the top right square and multiply together pairs of digits that meet. 4x3 is 12, so write the answer with the tens digit above the diagonal line and the ones below.
3. Continue across for each square and then do the same for the second row. When it is a single digit, eg 1x3, write 0 above the diagonal line.
4. Once the lattice is complete, start in the bottom right corner and look at the numbers in line separated by the diagonals. Working across and reading up, this is (2), (8, 3, 2), (6, 0, 3, 1), (1, 6, 0) and (0).
5. Add these diagonals up, writing the totals (in red) in line with each square. When the total goes beyond 9, carry the 1 and write it in the next diagonal.
6. Now read the number (in red) from top left down and across to bottom right.
It shows that 214 x 38 = 8132
Russian Peasant Method
This method for multiplying large numbers only involves halving, doubling and adding.
Follow this example for 45 x 26.
STEP 1
- Write each number at the top of a column.
- Keep halving the number in the left column until you reach 1. If it is an odd number, take away 1 and halve that number instead.
- Double the numbers in the right column for the same number of steps as in the left column.
STEP 2
- Cross out any even numbers in the left column and the corresponding numbers in the right column.
STEP 3
- Add the numbers in the right column that are not crossed out. This gives the answer to the multiplication.
While visiting a Ministry school in Abu Dhabi, the girls in a Y6 class were using what they called the ‘lattice method’, which I recognised as the Gelosia method for multiplying. The teacher was from the US and had this as her preferred standard method for long multiplication.
The girls could explain the method very clearly – even in broken English as Arabic speakers – but did not question why it worked. This is a problem with Napier’s Bones and the Gelosia method – a basic understanding of the method is not clear, unlike the grid method for multiplication which partitions and uses place value with transparency.
The advantage of the grid method is that the place value position is clear for children to see and this encourages real understanding of numbers and multiplication, rather than having a method that works but does not support children's understanding.
Some teachers interpret the 2014 NC PoS as only allowing the written method of mulitplication to be taught. This is the ultimate aim, to take children on to the formal vertical written method, however I believe that the grid method provides an important step in a child's understanding, which then leads on to the fformal vertical written method.