This was from a child who was good at maths, confident and quick to learn. However, he had obviously misunderstood something here. The teacher had explained the method for multiplying whole numbers by fractions to the class, but importantly had only explained it verbally. She had not used any models or images to represent the process and this is the main reason for the misunderstanding.
So, did you work out the method that the child was using?
It is worth considering the spoken process to see where the problem lies. The child would have heard something like: ‘Divide the whole number by the denominator and then multiply that by the numerator.’ What the child understood from this was: ‘Divide the whole number by the denominator and then multiply the denominator by the numerator. Add these together.’
Example: 2/3 of 15
15÷3 = 5
2x3 = 6
5+6 = 11
The same algorithm had been used for all the questions and involved some tricky calculations. He was handling mental division, multiplication and addition with no mathematical errors – it was the algorithm that was the problem.
There was also the moment for the child when answering 2/3 of 6 = 8 that alarm bells should have been ringing and he should have been thinking that this was just not possible.
Another interesting point is that this is an example of ‘intelligent practice’ or ‘procedural variation’, with fractions kept the same and the amounts altered. It shows a possible issue with this, if a child is repeating the same wrong method to answer each question.
I discussed this child’s work with the teacher and worked on changing the approach so that the children could explore multiplying whole numbers by fractions rather than simply being told the procedure. We also considered the use of appropriate models and images when demonstrating and clarifying the learning, to ensure a good understanding of the maths.
Explore
Using cubes as eggs to find fractions of a 12-space egg box was the starting point, with the children making posters of their results. They started with unitary fractions and then found fractions of 12 with numerators greater than 1, for example 2/3 of 12 = 8.
This led on to finding pairs of fractions that totalled ‘1 whole’ (eg 5/6 of 12 = 10 and 1/6 of 12 = 2) and on to equivalent fractions (eg 2/4 of 12 = 1/2 of 12).
Problem solving included working out the missing fraction, such as 4 = __ of 12 or 'What fraction of 12 is 4?'. The cubes were then used to find fractions of different amounts.
Clarify
Strips of card, like a bar model, with number tiles were used to demonstrate fractions of amounts. This reinforced the importance of starting by dividing the whole number into the number of parts shown by the denominator. The numerator then showed how many of these parts to take – a simple and effective model.
The teacher also gave the class some calculations that were incorrect and asked them to correct them and work out why they were wrong – always a useful activity for children.
There is a clear emphasis on the importance of the way the mathematics is represented to the learners to secure understanding. Have a read of this article on using a twenty-frame to represent addition for more on representation.
Dealing with questions as they arise from children requires flexibility, decision making and the ability to ‘think on your feet’ or ‘grab the moment’. Another important aspect of teaching effectively is not only recognising and dealing with misconceptions, but also listening and responding to the ideas from the class. From this, teachers will perhaps gain deeper subject knowledge by understanding the knowledge that children bring to the lesson and to listen to them as they take an active part in their learning.
This all illustrates the importance of teachers having a deep (pedagogical) subject knowledge of mathematics. Teaching mathematics effectively involves, amongst other things, a good understanding of mathematical concepts and skills, including dealing with misconceptions and individual needs and the ability to guide children in appropriate small steps forward in knowledge or understanding.
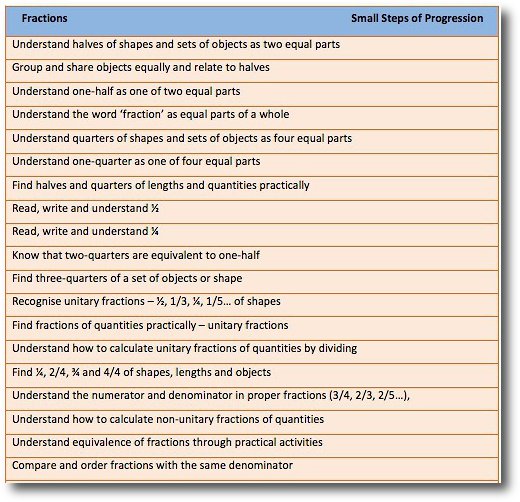
As a final point, here is an example of part of the Broadbent Maths progression steps for fractions. You can request samples of Broadbent Maths to view the resources and subscribe as a school.