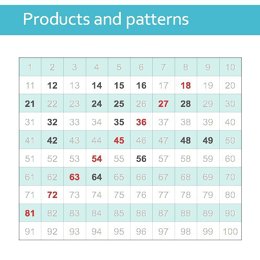
A multiplication sentence such as 3 x 4 = 12 is made up of two factors: the multiplicand (3) and the multiplier (4). These are multiplied together to give the product or multiple (12).
We often focus on the two factors of a multiplication sentence, however it is interesting to identify and focus on the products. If children begin to remember some of the key numbers that are products, then it will help to recall multiplication facts. We do it as adults without realising it.
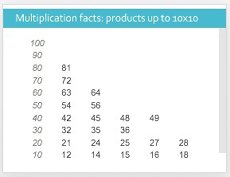
1. List all the multiples of 10 in a column up to 10x10 = 100.
These are usually easy for children to learn, so just check, ‘we know all these don’t we?’ Obviously sort out any difficulties children have with these numbers, but if there are I would suggest the activity may be a challenge at this stage.
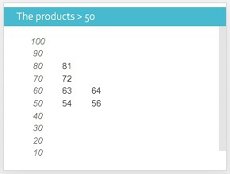
54, 56, 63, 64, 72 and 81
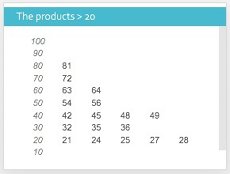
So if we focus on the products of the times tables up to 10x10 (and ignore multiples of 10),
there are only six key numbers for children to remember.
62 isn’t there, or 58… and many other numbers that shouldn’t enter our heads when we’re trying to quickly recall our tables facts.
I’ve used this as an activity with Y3-6 children and it really makes them think about these key numbers. Some of them have taken the numbers on the 100 square and circled one at a time to learn the facts associated with that product. It’s just a different and alternative way in to the quest to become quick recallers of our tables facts.
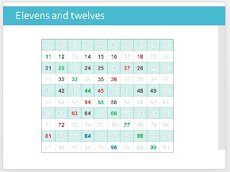
What about the 11 and 12 times tables?
True, these aren’t included, but in the ‘numbers to 100’ rule the 12 times table only adds two more numbers: 84 and 96. The multiples of 11 do add to the list, but the pattern is as easy as the multiples of 10 and is a nice tables pattern to learn.
A good way of learning the 12x table is to use the power of partitioning. Break it up into x10 and x2, which seems slow, but is actually a pretty quick way of recalling correctly (rapid speed isn’t everything!). For example, 7 x 12 = (7 x 10) + (7 x 2) = 84
The process is ‘7 times 10 then add double 7’ – which isn’t a bad way of playing with the numbers to develop number sense and fluency.