Spheres are often referred to having one face, cones two faces and cylinders three faces. Mathematically a face on a 3D shape is part of a plane and therefore is flat. Does this means that much of the language that has been used is inaccurate?
They went on to say that their staff had discussed their method for explaining that a sphere has a curved surface; a cone has 1 face and 1 curved surface etc. However, the definition of an edge is that it is where 2 faces meet. They were unsure how this could be explained and asked if I had any suggestions.
What a great question! I'm asked quite a lot about this and I remember when writing a maths dictionary some years ago that it was a point of contention between maths academics at the time. Some of the issues are because we want it defined for primary school use to make it accessible to our children.
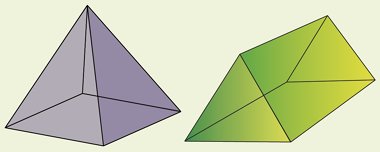
It is best to consider this by sorting shapes by their properties. Start with any 3D or solid shape and they can be classified as polyhedra and non-polyhedra.
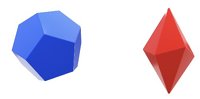
Now we can look at the other set of non-polyhedra, and these will include spheres, cones, cylinders and hemispheres. As these are not made with faces of polyhedra, then they include curved surfaces, faces and curved edges. This is where definitions get a little loose at primary level, but if you are consistent and make a clear distinction between surfaces and faces as well as edges and curved edges then this should be fine.
So, going back to the question from the school, they were just about spot on with their thoughts on this in their discussion:
- a sphere has a single curved surface and no edges or vertices.
- a cone has one curved surface, a flat face with a curved edge (usually, but not always, a circle) and an apex. To make it clearer, the face can be called a base and the point is the apex, not a vertex.
- a cylinder has one curved surface, two curved edges (always circles) and no vertices.
- a hemisphere has one curved surface, a flat face and a curved edge (always a circle).