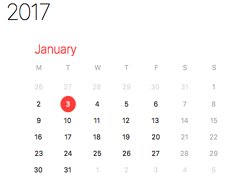
The 'doomsday rule' is a way to mentally calculate the day of the week for any date - without the use of a calendar. Looking at the patterns and rules and then using them to predict the day of any date gives children a reason to learn the order of months, the positional and ordinal number for each month, as well as developing a desire to play with numbers. A great maths motivator for the new year.
Mathematician John Conway noticed that some dates always fall on the same day of the week for any given year.
Once you know the day of the week for 3 January you know the day of the week for all these dates in the same year. In 2017 3 January is a Tuesday.
So let’s look at these key dates or 'doomsdays'. January and February stand alone and these are dates that just have to be remembered, but there are patterns and rules in the other dates that make them fairly easy to remember.
Once you know the day of the week for 3 January you know the day of the week for all these dates in the same year. In 2017 3 January is a Tuesday.
So let’s look at these key dates or 'doomsdays'. January and February stand alone and these are dates that just have to be remembered, but there are patterns and rules in the other dates that make them fairly easy to remember.
So let’s give it a try.
What day of the week is 18th August 2017?⇒ August is month 8, an even month
⇒ so 8/8 is a Tuesday
⇒18th August is 10 days after Tuesday 8/8/17
⇒ 10 days = 1 week + 3 days
⇒ so one week after 8/8 is a Tuesday and 3 more days …Wednesday, Thursday, Friday 18th August 2017 is a Friday.
Now write this second set of dates on the board. What patterns can you notice with these dates?
• These are all odd numbered months
• There is a difference of 4 between the day and the month in each date
In the first half of the year the difference is + 4 month number + 4 = day
In the second half of the year the diffference is - 4 month number - 4 = day
• These are all odd numbered months
• There is a difference of 4 between the day and the month in each date
In the first half of the year the difference is + 4 month number + 4 = day
In the second half of the year the diffference is - 4 month number - 4 = day
So let's give it a try
What day of the week is 2nd November 2017?⇒ November is month 11, in the second half of the year, so – 4
⇒ 11 - 4 = 7 so 7/11 is a Tuesday in 2017
⇒ 2nd November is 5 days before 7/11.
⇒ Count 5 days back from Tuesday…. Mon, Sun, Sat, Fri, Thursday 2nd November 2017 is a Thursday.
Children will enjoy showing off their skills at home for friends and family. They can find the day for their own birthday this year and then check it on a calendar. It is an exciting task to be able to calculate the day for any date and it is a great motivator to learn the order of months and their positional and ordinal numbers.
Extend the activity
Some of your higher attaining children may want to have a look why this works. Why is it that these key dates or 'doomsdays' are on the same day of the week every year? Give them time, maybe over a week, to look at the dates on a calendar and see what they can notice.
If they can't find any connections then explain that it works because the number of days between these dates are divisible by 7, or to put another way, have whole weeks between them.
Don't leave it there - ask your class to prove it. Look at a 2017 calendar and count the weeks between each date. Count the number of days between any two dates and check if it is divisible by 7.
I have provided a simple way to find a date in 2017 but there are far more complicated ways to calculate the date for any year.
There is a version that you might be interested in for yourself and you can see John Conway explaining it on YouTube. However, this is quite complex so for your class you can stick to naming the day of the week for any date in 2017.
Extend the activity
Some of your higher attaining children may want to have a look why this works. Why is it that these key dates or 'doomsdays' are on the same day of the week every year? Give them time, maybe over a week, to look at the dates on a calendar and see what they can notice.
If they can't find any connections then explain that it works because the number of days between these dates are divisible by 7, or to put another way, have whole weeks between them.
Don't leave it there - ask your class to prove it. Look at a 2017 calendar and count the weeks between each date. Count the number of days between any two dates and check if it is divisible by 7.
I have provided a simple way to find a date in 2017 but there are far more complicated ways to calculate the date for any year.
There is a version that you might be interested in for yourself and you can see John Conway explaining it on YouTube. However, this is quite complex so for your class you can stick to naming the day of the week for any date in 2017.
Related articles
A Special date with consecutive square numbers
4th September 2016 was a square day! 4.9.16. Explore other square days.
Consecutive dates - an investigation adding 3 consecutive numbers
11.12.13 was a special date with consecutive numbers.
Palindromic dates - how many can you find?
21.11.12 or 31.1.13 - will there be any palindromic dates in the next year?
All about 15 maths activities for 15.12.15
These ideas can be adapted... 16 minutes of maths for 16th of September, October, November or December 2016.
This includes finding Fibonacci numbers in nature, exploring patterns and rules in number sequences, sunflowers and cones
2013 was the first year not to have a repeating digit since 1987
When will be the next time that a year has a repeating digit?
A Special date with consecutive square numbers
4th September 2016 was a square day! 4.9.16. Explore other square days.
Consecutive dates - an investigation adding 3 consecutive numbers
11.12.13 was a special date with consecutive numbers.
Palindromic dates - how many can you find?
21.11.12 or 31.1.13 - will there be any palindromic dates in the next year?
All about 15 maths activities for 15.12.15
These ideas can be adapted... 16 minutes of maths for 16th of September, October, November or December 2016.
This includes finding Fibonacci numbers in nature, exploring patterns and rules in number sequences, sunflowers and cones
2013 was the first year not to have a repeating digit since 1987
When will be the next time that a year has a repeating digit?